机器学习在企业风险管理中的应用举例
前言

什么是学习? 维基百科上说学习是获得新的理解、知识、行为、技能、价值观、态度和偏好的过程。在计算技术快速发展的今天,让机器去利用算法和算力去“学习”、推理、决策,就是机器学习。 机器学习按照学习的方式可以分为以下几种,但也不绝对,存在半监督学习和强化学习这种难以归类的方式,部分算法也可以横跨几种分类:
Figure 1: 一些常见的机器学习算法
机器学习深究的话,需要学习很多数学和计算机。但是工业界将常用的机器学习算法封装地很好(pytorch, scikit-learn),几行代码就可以实现一个模型, 之后便是漫无止境地调参 。
本文主要参考了Pedregosa et al. (2011)的文档,在编码过程中阅读文档是有帮助的。
机器学习在企业风险管理中的应用
Mai et al. (2019) 利用 CNN 预测企业破产,在处理文本数据时利用 word embedding 量化,AUC 曲线如图

Golbayani, Florescu, and Chatterjee (2020) 使用决策树、随机森林、支持向量机和多层感知器应用于相同的数据集,预测公司未来评级。他们统计了机器学习在债券评级和公司信用评级方面的文章,很多认为 SVM 和神经网络是比较准确的。但是他们使用 Notches Distance 来对机器学习绩效来打分,认为基于决策树的两种方法更有效。
Kellner, Nagl, and Rösch (2022) 利用神经网络预测违约损失 Loss Given Default 将传统的分位数回归的回归元作为第一层,通过神经网络揭示其中的非线性关系,比如交叉项及其他非线性关系,神经网络最后一层是传统的分位数回归。利用 first order feature importance,量化输入变量的整体重要性。同时排除掉二阶的和交互的在分位数中接近于零。因此 QRNN 和分位数 QR 的分位数损失非常相似 通过允许分位数回归神经网络实现的分位数中的非线性和相互作用来扩展这种方法。这种方法大大增强了建模的灵活性。额外的灵活性在更好地分布拟合和超时样本方面带来了回报,分位数预测精度提高了 30%。同时更加 robust 。
当前机器学习最火热的两个应用方向是计算机视觉 CV 和自然语言处理 NLP ,亦有一些文献利用自然语言处理分析文本数据做研究。
机器学习预测信用评级
数据说明
A list of 2029 credit ratings issued by major agencies such as Standard and Poors to big US firms (traded on NYSE or Nasdaq) from 2010 to 2016.
There are 30 features for every company of which 25 are financial indicators. They can be divided in:
-
Liquidity Measurement Ratios: currentRatio, quickRatio, cashRatio, daysOfSalesOutstanding
-
Profitability Indicator Ratios: grossProfitMargin, operatingProfitMargin, pretaxProfitMargin, netProfitMargin, effectiveTaxRate, returnOnAssets, returnOnEquity, returnOnCapitalEmployed
-
Debt Ratios: debtRatio, debtEquityRatio
-
Operating Performance Ratios: assetTurnover, fixedAssetTurnover
-
Cash Flow Indicator Ratios: operatingCashFlowPerShare, freeCashFlowPerShare, cashPerShare, operatingCashFlowSalesRatio, freeCashFlowOperatingCashFlowRatio
1 2 3 4 5import pandas as pd # df = pd.read_csv("./corporate_rating.csv", encoding="utf-8") df = pd.read_csv("/Users/dcy/Code/erm/corporate_rating.csv", encoding="utf-8") df.info()1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38<class 'pandas.core.frame.DataFrame'> RangeIndex: 2029 entries, 0 to 2028 Data columns (total 31 columns): # Column Non-Null Count Dtype --- ------ -------------- ----- 0 Rating 2029 non-null object 1 Name 2029 non-null object 2 Symbol 2029 non-null object 3 Rating Agency Name 2029 non-null object 4 Date 2029 non-null object 5 Sector 2029 non-null object 6 currentRatio 2029 non-null float64 7 quickRatio 2029 non-null float64 8 cashRatio 2029 non-null float64 9 daysOfSalesOutstanding 2029 non-null float64 10 netProfitMargin 2029 non-null float64 11 pretaxProfitMargin 2029 non-null float64 12 grossProfitMargin 2029 non-null float64 13 operatingProfitMargin 2029 non-null float64 14 returnOnAssets 2029 non-null float64 15 returnOnCapitalEmployed 2029 non-null float64 16 returnOnEquity 2029 non-null float64 17 assetTurnover 2029 non-null float64 18 fixedAssetTurnover 2029 non-null float64 19 debtEquityRatio 2029 non-null float64 20 debtRatio 2029 non-null float64 21 effectiveTaxRate 2029 non-null float64 22 freeCashFlowOperatingCashFlowRatio 2029 non-null float64 23 freeCashFlowPerShare 2029 non-null float64 24 cashPerShare 2029 non-null float64 25 companyEquityMultiplier 2029 non-null float64 26 ebitPerRevenue 2029 non-null float64 27 enterpriseValueMultiple 2029 non-null float64 28 operatingCashFlowPerShare 2029 non-null float64 29 operatingCashFlowSalesRatio 2029 non-null float64 30 payablesTurnover 2029 non-null float64 dtypes: float64(25), object(6) memory usage: 491.5+ KB
评级分布如下图。我们可以看到评级 CC, C, D 的企业数量较少。三大评级公司所谓的“D”是违约“Default”,因此我们保留下来 D 级,而合并 CCC CC C 。一方面是由于 CCC 以下数量少,另一方面是由于大多数“评级下调加速到期”条款限定在了降至 CCC 的垃圾级。类似的,由于 AAA 企业数量很少都是非常优质的企业( 不像目前国内评级新发债一半为 AAA ),而 AA 和 A 数量都不小,我们仍然单独把他们拿出来。
|
|
|
|

让我们处理一下数据
|
|
|
|
get_score 中定义了三重维度来度量预测的准确性,如下表。precision 是 \(tp / (tp + fp)\) ,即预测阳性中真实为正的概率;recall 是 \(tp / (tp + fn)\) ,即样本中的正例有多少被预测正确了;而 f1 则是二者的调和平均
| True | False | |
|---|---|---|
| Positive | TP | FP |
| Negative | TN | FN |
鉴于评级有七个,完完全全的准确率可能没有那么高,我们做一个随机的测试,作为基准。
|
|
| precision | : | 0.23640721599080028 | recall | : | 0.12547244094488194 | f1 | : | 0.1544436285781241 | \(R^2\) | : | 0.008907176874420717 |
线性回归与决策树
我们先看一些简单直接的例子。
按照维基百科的定义,我们在计量经济学中学习的 OLS/GLS/Logit 模型也是通过机器来学习拟合样本的分布,也是一种机器学习。统计学中的 lasso/ridge 等回归方式也在模型泛化中有许多应用。
|
|
|
|
| precision | : | 0.18152641834788635 | recall | : | 0.2440944881889764 | f1 | : | 0.15470492292394605 | \(R^2\) | : | -0.01775335686060572 |
决策树也在日常生活中有应用,车险定价或者我们日常的决策都可以抽象成决策树。 他的思想是,一个数据集有多个特征,每个节点按照某个特征是否满足一定的条件分叉,形成一棵二叉树。 该节点选取特征分叉的决策依据是最大化“信息增益”,即分叉前后数据更“有序”,且更有序的程度最大,常见指标的有信息熵/基尼系数等。 这棵树为了避免过拟合,我们会对决策树“剪枝”,增加一些分支条件的限制,可以看这里。
决策树好处是计算量简单,可解释性强,比较适合处理有缺失属性值的样本,能够处理不相关的特征;但是容易过拟合。
|
|
| precision | : | 0.3498883972871522 | recall | : | 0.3799212598425197 | f1 | : | 0.3528756642882673 | \(R^2\) | : | 0.3632276367156315 |
集成学习
ensemble learning 是单个模型并不能很完美的解决某个分类或者回归问题(弱监督模型,在某些方面表现较好)的时候,那么就训练出多个弱监督模型,每个模型可能是相同的也可以是不同的,然后预测的时候将数据分别输入每个模型,最后将每个模型的输出综合起来作为该未知数据的输出即便某一个弱分类器得到了错误的预测,其他的弱分类器也可以将错误纠正回来。简而言之,采样-学习-组合。
如何训练和输出呢?
bagging
Bagging是bootstrap aggregating的简写。在 bagging 方法中,从整体数据集中采取有放回抽样得到N个数据集,在每个数据集上学习出一个模型。
随机森林就是采用了 bagging 的方式训练了许多棵决策树,是为“森林”。在输出时,每一棵树都将其结果“投票”,哪个类别多,输入样本就属于哪个类别。
|
|
| precision | : | 0.39603489727136376 | recall | : | 0.4251968503937008 | f1 | : | 0.38351839772007446 | \(R^2\) | : | 0.39959139741930844 |
Bagging主要关注降低方差,因此它在不剪枝的决策树、神经网络等学习器上效用更为明显,不容易过拟合。
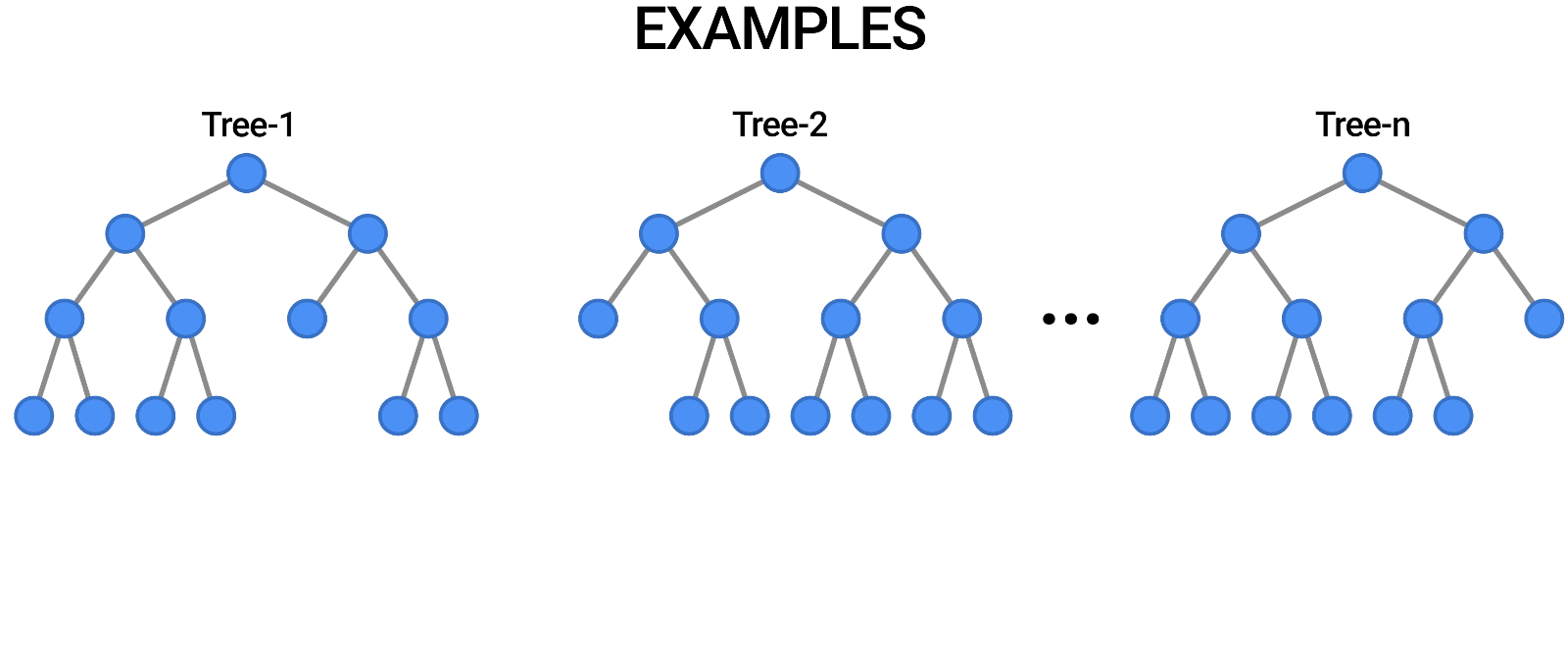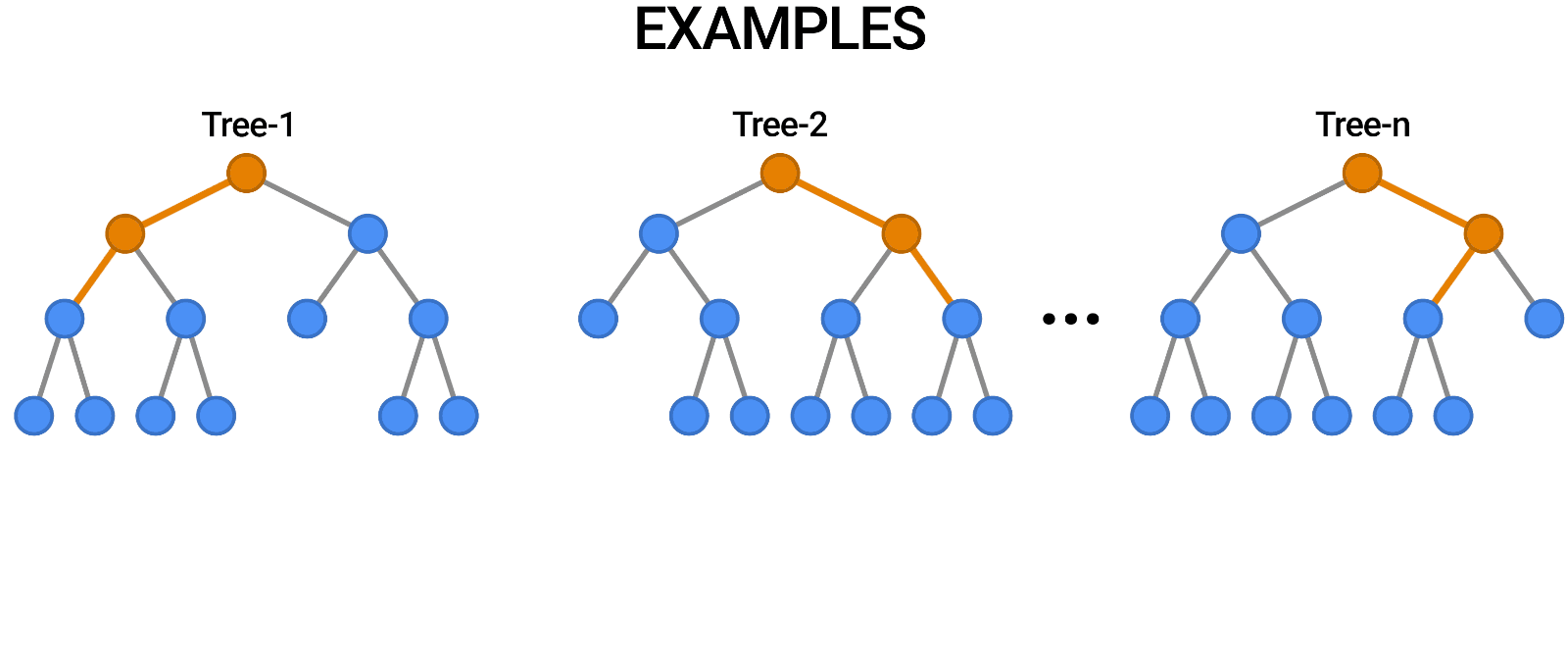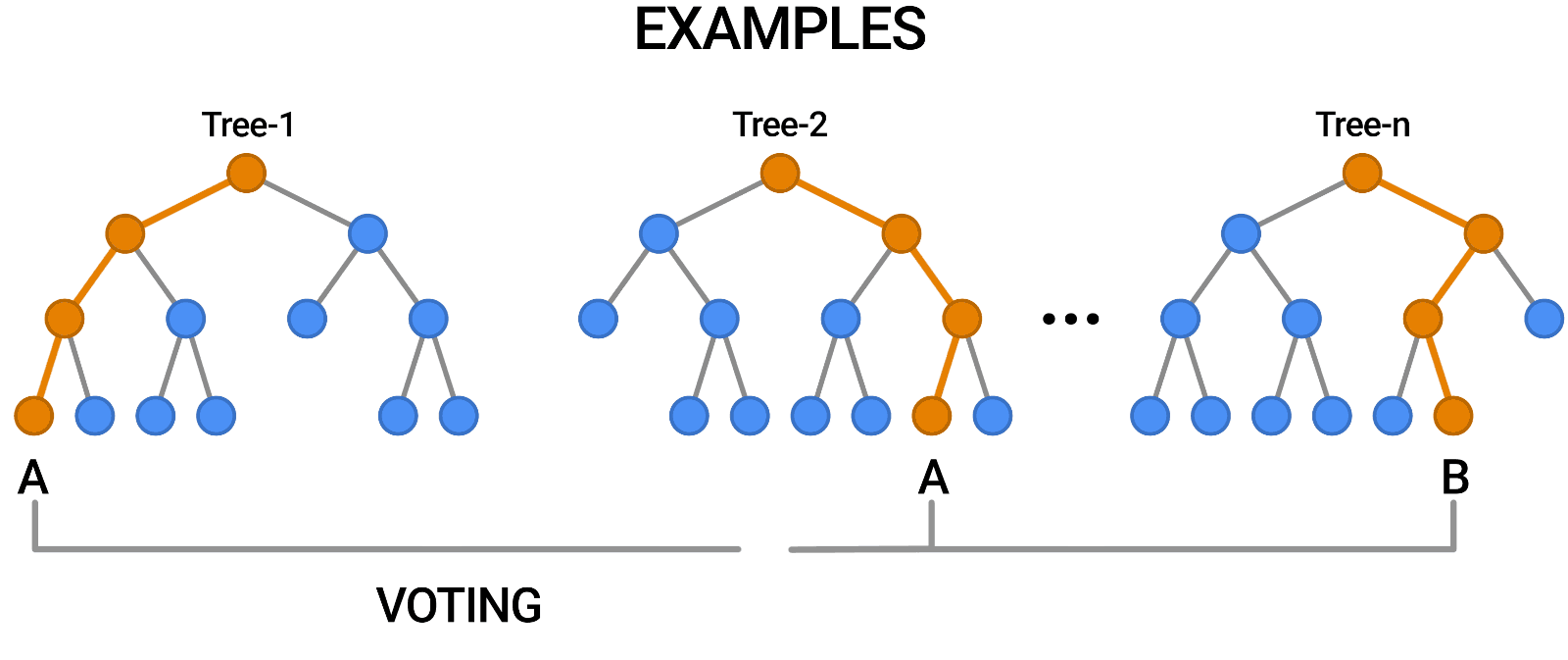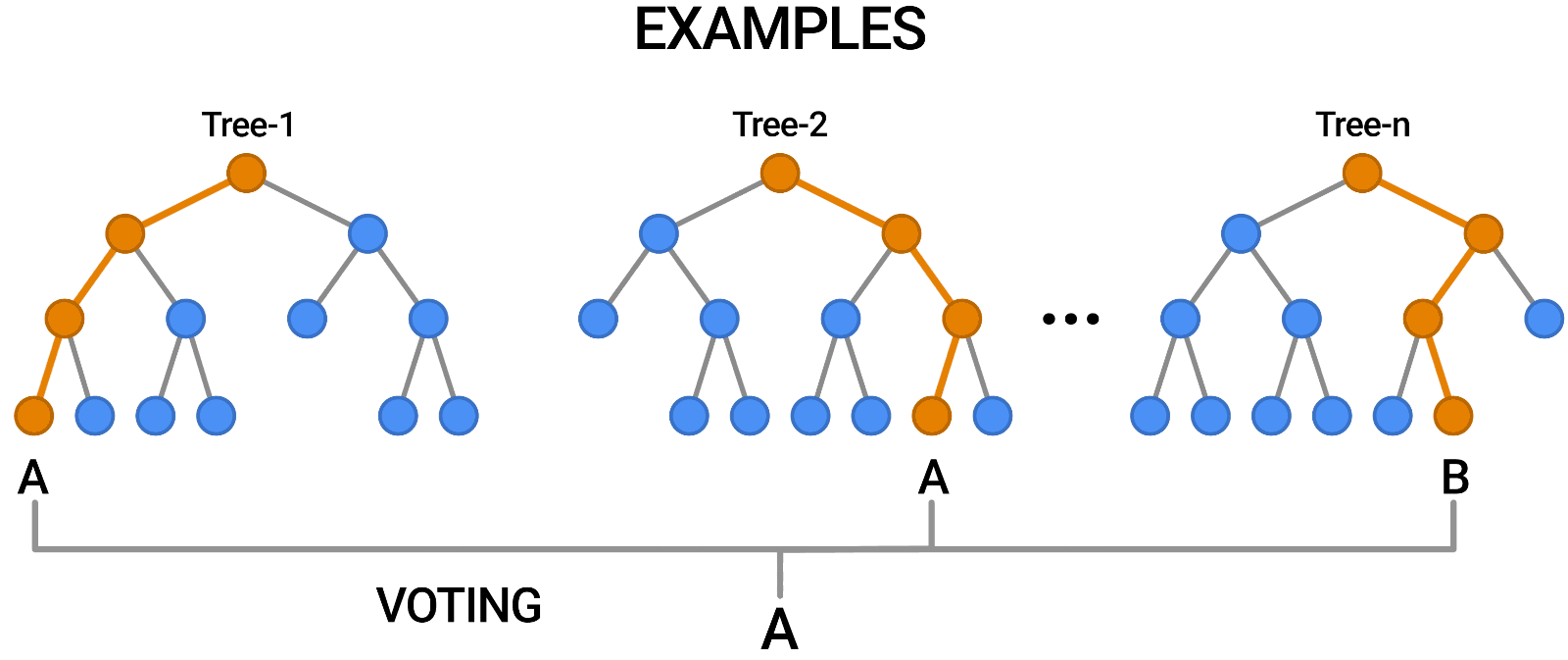
Figure 2: random forest
boosting
bagging 的训练是平行的,boosting 则是迭代地训练一系列的分类器,每个分类器采用的样本分布都和上一轮的学习结果有关,直观比方是每个树都去学习上一个树没有学习好的地方,代表算法有AdaBoost(Adaptive boosting)算法,以及 XGBoost 算法。
调参时可以树的深度很少就能达到很高的精度。

|
|
| precision | : | 0.530520009176101 | recall | : | 0.5255905511811023 | f1 | : | 0.5094674767985568 | \(R^2\) | : | 0.5421094375792002 |
支持向量机
Support Vector Machine, SVM 是一种二分类器,其思想是样本分布在空间中,找到一个可以划分开样本点、并且间隔最大的的(超)平面。直观上间隔最大是为了让模型更稳健。
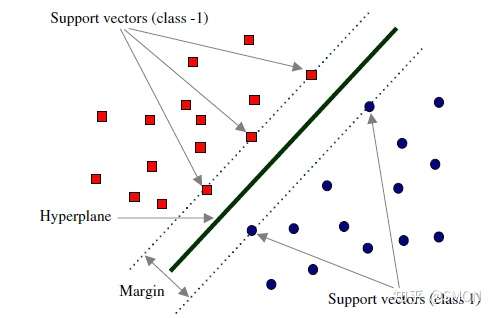
Figure 3: SVM 图示
最简单的线性的硬间隔可分的如图 [3](#figure–SVM 图示) 所示,当然这是比较理想的情况。当样本分布更复杂的时候,我们会选择软间隔,即将之前的硬间隔最大化条件放宽一点,允许部分点出错,在优化函数中加入惩罚项。
如果还是不可以,我们会运用核函数来推导到非线形的情况,简单说就是将低维的样本点映射到高维空间,使样本线性可分。例如内积平方的核函数,\(K(v_1,V_2)=(x_1x_2+y_1y_2)^2\),可以看作是三维空间中 \((x_i^2,\sqrt{2}x_iy_i,y_i^2)\) 两个点之间的距离
|
|
| precision | : | 0.4136927083234441 | recall | : | 0.4094488188976378 | f1 | : | 0.351708147106921 | \(R^2\) | : | 0.3431290118925812 |
KNN
这里的 NN 不是后文的 CNN 等的神经网络,全称是K Nearest Neighbors,意思是某个点分类取决于 K 个最近的邻居
|
|
| precision | : | 0.3625400456087721 | recall | : | 0.35236220472440943 | f1 | : | 0.34202311550427716 | \(R^2\) | : | 0.29873782865224163 |
K means
有四个牧师去郊区布道,一开始牧师们随意选了几个布道点,并且把这几个布道点的情况公告给了郊区所有的村民,于是每个村民到离自己家最近的布道点去听课。
听课之后,大家觉得距离太远了,于是每个牧师统计了一下自己的课上所有的村民的地址,搬到了所有地址的中心地带,并且在海报上更新了自己的布道点的位置。
牧师每一次移动不可能离所有人都更近,有的人发现A牧师移动以后自己还不如去B牧师处听课更近,于是每个村民又去了离自己最近的布道点……
就这样,牧师每个礼拜更新自己的位置,村民根据自己的情况选择布道点,最终稳定了下来。
之前提到的算法都需要对数据进行一定的标注,标好某些数据属于某个分类,也就是常说的“监督学习”。K-means 是一种无监督学习,我们不需要声明训练中的哪些数据是哪个分类。
K-means 的方法是,选择初始化的 k 个样本作为初始聚类中心 \(a_i\) ,针对数据集中每个样本 \(x_i\) 计算它到 k 个聚类中心的距离,并将其分到距离最小的聚类中心所对应的类中;重新计算每个类别的质心作为聚类中心 \(a_i\) ,再重复上面的过程,直至聚类中心“稳定”下来。
|
|
深度学习/神经网络
深度学习以神经网络为基础。神经网络是一种模仿生物神经系统结构和功能的数学模型,对函数进行估计和近似。
多层感知机
是深度学习的入门算法,误差反向传播 Backpropagation,刺激正向传播后通过梯度下降的方式最小化误差反向传播更新权值(最小化的方式是“梯度下降”)。它的信息处理能力来源于简单非线性函数的多次复合。
-
梯度下降与反向传播
我们用最小二乘法来理解“梯度下降”和“反向传播”
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18import torch x = torch.rand([500,1]) # X 是一个 tensor ,可以把他想象成 500x1 的向量 y_true = 3*x+8 learning_rate = 0.05 # learning rate 是每次梯度下降的“步长” w = torch.rand([1,1], requires_grad=True) # w 和 b 我们要 pytorch 自动求导 b = torch.tensor(0, requires_grad=True, dtype=torch.float32) for i in range(500): y_pred = torch.matmul(x,w)+b # 预测是多少 loss = (y_true-y_pred).pow(2).mean() # 损失 if w.grad is not None: # 把上一次的梯度清零 w.grad.data.zero_() if b.grad is not None: b.grad.data.zero_() loss.backward() # 误差反向传播,得到 w 和 b 的梯度 w.data = w.data - w.grad*learning_rate # 梯度下降找到新的 w 和 b b.data = b.data - b.grad*learning_rate if i % 50 == 0: print(w.item(), b.item(), loss.item())1 2 3 4 5 6 7 8 9 101.3611265420913696 0.907298743724823 82.69320678710938 4.225016117095947 7.326720714569092 0.1297740489244461 3.884570360183716 7.520116806030273 0.06721365451812744 3.6368446350097656 7.654516220092773 0.03483818471431732 3.4584925174713135 7.7512712478637695 0.01805729605257511 3.3300886154174805 7.820929527282715 0.009359428659081459 3.2376456260681152 7.8710784912109375 0.004851202480494976 3.1710915565490723 7.90718412399292 0.00251445802859962 3.123175859451294 7.933177947998047 0.0013032826827839017 3.088679552078247 7.951891899108887 0.0006755132926627994上述的代码在 pytorch 中对应的有:
for循环里面的模型nn.Module封装好了许多模型loss的定义torch 中也有多种计算方式 loss的计算优化器 nn.optim中提供了许多优化器通过 pytorch 我们可以写成
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23import torch from torch import nn from torch import optim x = torch.rand([50,1]) y = 3*x+8 class Lr(nn.Module): def __init__(self): super(Lr, self).__init__() self.layer = nn.Linear(1,1) def forward(self, x): return self.layer(x) model = Lr() criterion = nn.MSELoss() optimizer = optim.SGD(model.parameters(), lr=0.05) for i in range(500): out = model(x) loss = criterion(y, out) optimizer.zero_grad() loss.backward() optimizer.step() list(model.parameters())
-
激活函数

神经网络本意是想模仿神经元。高中我们学过神经受到刺激后不一定会产生电信号,而是需要达到阈值后才能产生动作电位。因此当神经网络的输入层收到信号传导给隐藏层后,隐藏层是直接向输出层传导(这样的话通过神经网络线性函数的叠加仍然是一个线性函数),而是要经历一个非线性的“激活函数”,如
relu,sigmoid,softsign,然后再进行传导。即针对 \(X\) 输入,神经元输出会是 \(f(W^TX+b)\) 。我们可以在这里可视化地理解一下 https://playground.tensorflow.org/
一层神经网络可以拟合出任意的函数,而多层的神经网络在拟合时更有效率
-
一个尝试
这是我用两层神经网络的代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29from torch import nn import torch torch.manual_seed(42) Ytrain_nn = pd.get_dummies(Ytrain) encode = Ytrain_nn.columns Ytrain_nn = torch.tensor(Ytrain_nn.values, dtype=torch.float32) Xtrain_nn = torch.tensor(Xtrain.values, dtype=torch.float32) hidden_layer = 40 net = nn.Sequential( nn.Linear(Xtrain_nn.shape[1], hidden_layer), nn.ReLU(), nn.Linear(hidden_layer, len(encode)), nn.Softmax(dim=1), ) optimizer = torch.optim.SGD(net.parameters(), lr=0.001) loss_func = torch.nn.MSELoss() for t in range(10000): prediction = net(Xtrain_nn) loss = loss_func(Ytrain_nn, prediction) optimizer.zero_grad() loss.backward() optimizer.step() Xtest_nn = torch.tensor(Xtest.values, dtype=torch.float32) prediction = pd.DataFrame(net(Xtest_nn).detach().numpy()) Ypredict = prediction.idxmax(axis=1).map(lambda x: encode[x]) result["bp neural network"] = get_score(Xtest, Ytest, lambda _: Ypredict) result["bp neural network"]precision : 0.27389121797460775 recall : 0.33858267716535434 f1 : 0.27631891749192855 \(R^2\) : -0.0591120710799986
CNN
所谓卷积神经网络,就是用卷积核扫描,类似“锐化”,是一种比较经典的计算机视觉算法。图片之间的像素是有关系的,刚刚的神经网络显然没有考虑到连续像素的关联性,CNN 通过做卷积将关系呈现出来。

卷积有其数学定义 \((f*g)(n) = \int_{-\infty}^{\infty}f(\tau)g(n-\tau)\mathrm{d}\tau\),简单地理解就是两个函数 f 和 g ,先对g函数进行翻转,相当于在数轴上把 g 函数从右边“卷”到左边去。然后再把 g 函数平移到 n ,在这个位置对两个函数的对应点相乘,然后相加(“积”)。
卷积神经网络先用卷积层扫描出特征,然后利用“池化”增强稳健性防止过拟合,最后一个全连接层处理输出。图像可以由二维的位置和第三维(颜色 RGB )确定,在 pytorch 中常用 Conv2d 。而我们的数据则是一条条的,望文生义应该用 Conv1d (其实会用在自然语言处理中,但 RNN 应用更多)。
从这里开始利用 CPU 训练比较慢,有 NVIDIA GPU 的同学可以尝试在 GPU 上训练
|
|
|
|
| precision | : | 0.4275809716701871 | recall | : | 0.4645669291338583 | f1 | : | 0.43998424878311354 | \(R^2\) | : | 0.43565444166649087 |
增加网络层数可能会导致梯度离散和梯度爆炸的情况,反而效果不好。残差网络 ResNet 利用在网络间加入 shortcut ,使更深层次的训练结果至少不差于更浅层次(如果更差就直接走 shortcut )
RNN
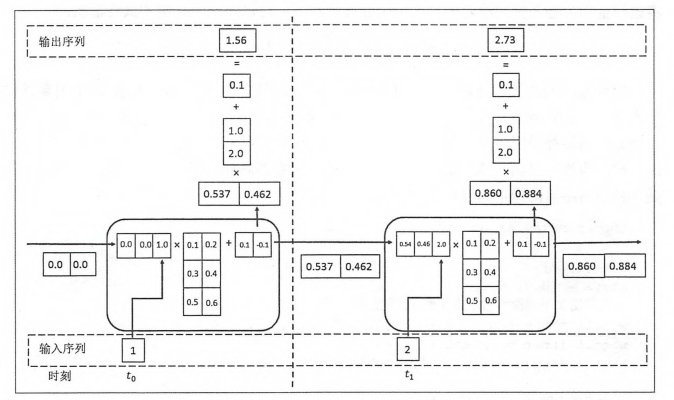 循环神经网络:常用在 NLP 中并大放异彩,也会应用在股价等时间序列中。他会短期地“记住”参数,就如同我说这句话的时候你短期地记住了上一句话,会更新“自我”而非直接向前传递,在该层中“循环”。即对于隐藏层而言,\(h_t = f_w(h_{t-1}, x_t)\) 。随着输入的更新,有一个短暂的 memory ,记住刚刚的参数。
循环神经网络:常用在 NLP 中并大放异彩,也会应用在股价等时间序列中。他会短期地“记住”参数,就如同我说这句话的时候你短期地记住了上一句话,会更新“自我”而非直接向前传递,在该层中“循环”。即对于隐藏层而言,\(h_t = f_w(h_{t-1}, x_t)\) 。随着输入的更新,有一个短暂的 memory ,记住刚刚的参数。
|
|
|
|
| precision | : | 0.45571789744910574 | recall | : | 0.4645669291338583 | f1 | : | 0.45579366963021595 | \(R^2\) | : | 0.3853397572978466 |
但是 RNN 的的梯度非常容易“爆炸”(特别大)或“离散”(特别小以致于不更新),预测可能会出错。
针对此,LSTM (Long Short Term Memory)模型设计了三个“门”:输入门 i ,遗忘门 f ,输出门 o ,有一篇非常好的blog详细描述了这些门是如何工作的,简而言之他加入了长期记忆的部分。
GAN & RL
- 生成对抗网络:随机取样作为输入,其输出结果需要尽量模仿训练集中的真实样本,使判别网络无法判断生成网络的输出结果是否真实
- 强化学习:博弈论……
强化学习(RL)是机器学习的一个领域,涉及软件代理如何在环境中采取行动以最大化一些累积奖励的概念。该问题由于其一般性,在许多其他学科中得到研究,如博弈论,控制理论,运筹学,信息论,基于仿真的优化,多智能体系统,群智能,统计和遗传算法。。在运筹学和控制文献中,强化学习被称为近似动态规划或神经动态规划。–Wikipedia
对比
|
|
| model | precision | recall | f1 | \(R^2\) |
|---|---|---|---|---|
| random | 0.2364 | 0.1255 | 0.1544 | 0.0089 |
| logit | 0.1815 | 0.2441 | 0.1547 | -0.0178 |
| decision tree | 0.3499 | 0.3799 | 0.3529 | 0.3632 |
| random forest | 0.396 | 0.4252 | 0.3835 | 0.3996 |
| gradient boosting | 0.5305 | 0.5256 | 0.5095 | 0.5421 |
| SVM | 0.4137 | 0.4094 | 0.3517 | 0.3431 |
| KNN | 0.3625 | 0.3524 | 0.342 | 0.2987 |
| bp neural network | 0.2739 | 0.3386 | 0.2763 | -0.0591 |
| CNN | 0.4276 | 0.4646 | 0.44 | 0.4357 |
| RNN | 0.4557 | 0.4646 | 0.4558 | 0.3853 |
|
|
